Quantum Roulette and the Nature of Reality

An interactive exploration of Bell's theorem, the strangest result in quantum physics

---

A new casino has opened up in the small town of Bellville, California—and it’s owned by Ronnie the Bear, who is suspected of having mob connections. You’re an inspector for the California Gaming Bureau, and you and your fellow inspector Fatima are heading up to Bellville to check out the casino before it opens, because you know Ronnie is probably up to something.

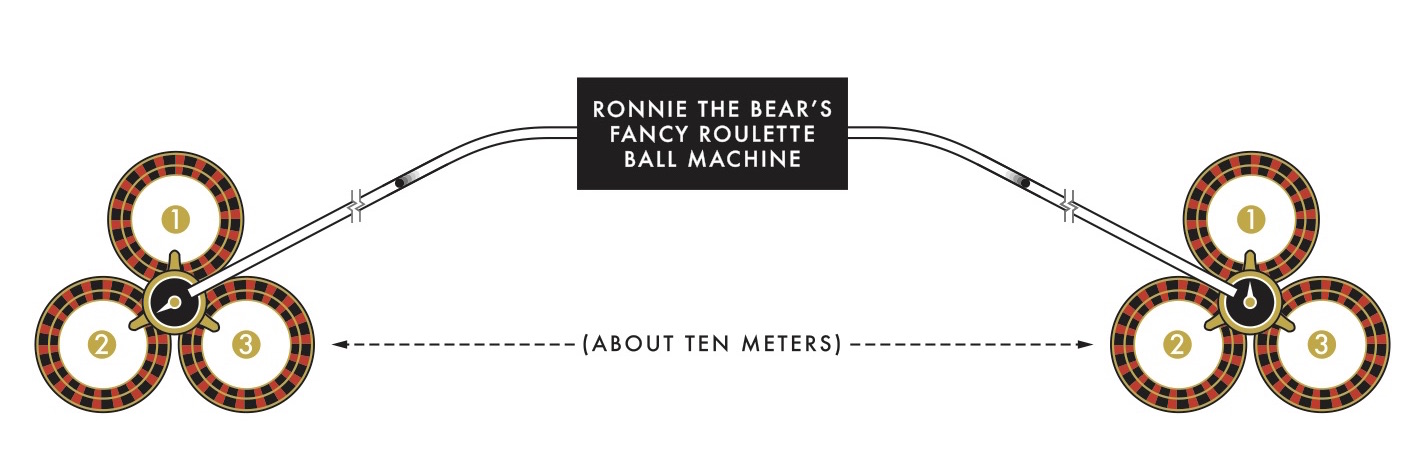
When you get there, you find that Ronnie’s casino floor has an overcomplicated roulette setup. In the center of the room is a large machine, with a chute extending out from each side to the roulette tables at either end of the floor. At each of the two roulette tables, there are three roulette wheels, with a smaller spinning dial in the center. In accordance with state law, the roulette wheels only have alternating squares of red and black on them, not numbers—roulette wheels with numbers on them are illegal in the state of California. (Really.) Once you and Fatima are each seated at one of the tables, you each select one of the three wheels in front of you. Then Ronnie presses a button on the machine, and a roulette ball appears in each of the chutes, rolling toward the tables.

You know Ronnie must be up to something with this overly-elaborate setup—you’re just not sure what. So you run the casino’s roulette machine many times over, choosing the wheels at each table randomly after the balls have been released, and you and Fatima each record the results at your table in your notebooks for later analysis.

When you get back to the hotel room, away from Ronnie’s prying eyes and security cameras, you and Fatima pore over your notes. You find that each table’s roulette wheels really do seem completely random—red and black each come up almost exactly half the time. But when you and Fatima compare your notebooks, the two of you immediately see something is fishy. “Look,” Fatima says. “Every time we used the same wheels at our tables, the roulette balls landed on the same colors!” You head back to the casino after hours to check things out.

Fatima is definitely right. And you also confirm that balls in matching wheels definitely land on matching colors even when you pick the wheels after the balls are on their way to the wheels.

Ronnie must be cheating! How? You and Fatima talk it over. The roulette balls always pick the same colors at the same roulette wheels, even when the wheels are chosen while the balls are en route. Therefore, the roulette balls must be coordinating their decisions in advance somehow—before they even leave the central machine, the roulette balls must have matching instruction sets that tell them both to do the same things when they arrive at each of the three wheels.

But then Fatima notices a second pattern in the results. “Look at these results,” she says.

“Ignore the times when we used the same wheels,” she says. “There’s something funny going on.” “Okay,” you say. “What is it?”

“When the wheels don’t match, the colors only match 25% of the time,” Fatima says.

“Are you sure?” you ask. “Yep, pretty sure,” she replies. “Check it out for yourself—if you run the casino over and over again, the number of times when the colors match even though the wheels don’t match always comes out to be about 25%.”

“OK,” you say, “I believe you. But so what?” “That number, 25%—it’s impossible,” Fatima says. “They have to match more than that if the roulette balls are sharing instruction sets.” Fatima rips a page out of her notebook and starts scribbling on it.
“There are only eight different possible instruction sets that the roulette balls can be carrying. Here they are.”

The problem, Fatima points out, is that they all have matching colors more than 25% of the time for mismatched wheels.

If the two roulette balls are sharing either of the instruction sets in the top group, then they’ll match 100% of the time, even when they end up in differently-numbered wheels. And if the two roulette balls are sharing one of the instruction sets in the bottom group, then when you and Fatima are using differently-numbered wheels, the balls should land on the same color one-third (33%) of the time.

“For example, say the instruction set is the one on the lower left,” Fatima says. “Then you and I will get different colors if we’re using wheels 1 and 2, or 1 and 3. But we’ll get the same color if we’re using wheels 2 and 3. So we get the same color for one out of the three possible pairs of mismatched wheels.”

“One out of three is one-third: 33%,” she continues. “And all the other instruction sets in the lower group work the same way. So if these roulette balls are carrying instruction sets, we should be getting the same color when we have mismatched wheels at least 33% of the time.”

With a sinking feeling, you realize that Fatima is right. “How are we getting 25%? How can it be that low?”

“I have no idea,” says Fatima slowly. “Ronnie has done...something really weird. Maybe the roulette balls are deciding what color to land on after they arrive at the roulette wheels, and they can communicate with each other somehow? They’d have to communicate really fast, though. Tiny radios?”

You mull this over. “Yeah, I guess that could work. They have to be coordinating somehow, otherwise they wouldn’t be able to guarantee that they always land on the same color when they arrive at matching wheels.”

“Exactly,” Fatima says. “But they can’t be coordinating that in advance—otherwise we’d see matching colors with mismatched wheels at least 33% of the time. So they must be connected somehow, at a distance.”

Whatever’s going on, one thing’s for sure: Ronnie has got you good this time.

---

Quantum roulette

Ronnie’s casino actually exists. But the roulette balls there are not really roulette balls—they’re pairs of photons, tiny packets of light. The roulette wheels are polarizers, machines that measure polarization (a property of light) along three different directions, selected randomly while the photons are in flight toward the machines. The two photons in each pair are “entangled” with each other, which is a term from quantum physics that just means the photons behave in the bizarre way described in the story about Ronnie’s casino. And Bell’s theorem is the proof embedded in the story, the one that you and Fatima figured out.

Just as in the story about the casino, there’s something strange going on with these photons, and it can’t be accounted for by assuming the photons have hidden instructions that they carry with them from the moment they separate. And entangled photons really do behave this way, so something very strange must be going on in quantum physics. But what, exactly, did Bell prove? To understand this, let’s take a closer look at what happened at Ronnie’s casino.

We started out with the assumption that roulette balls can’t magically communicate with each other instantaneously across long distances (though we never explicitly stated this until the end). Physicists call this no-instantaneous-signaling assumption “locality.” This idea of locality led us to the conclusion that there must be hidden instruction sets in the roulette balls themselves, because that was the only way to account for the perfectly matched outcomes when you and Fatima used the same roulette wheels. But the fact that your outcomes didn’t match more than 25% of the time when you didn’t use the same wheel as Fatima ruled out the possibility of hidden instructions. Therefore, something must be wrong with our assumption: locality must be violated.

In the case of Ronnie’s casino, the roulette balls could still be communicating by radio. But in real experiments, the roulette balls are photons traveling at the speed of light. Those photons are heading to two polarizers that can be very far apart—in some experiments, as far as hundreds of kilometers. Once one photon arrives at a polarizer, no light-speed signal could possibly reach the other photon before it too reaches a polarizer and makes its decision about what to do. In short, the results of real experiments with entangled photons mean that something, some influence, is going faster than light. Entanglement is not just an artifact of the mathematics of quantum physics: it’s a real phenomenon, an actual instantaneous connection between far-distant objects. (It provably cannot be used for faster-than-light signaling, though—to do that, you’d need to be able to control which color each roulette ball landed on at the casino.)

This is an astonishing result. How can it be right? Relativity dictates that faster-than-light signals are impossible, on pain of paradox. And relativity is one of the best-tested and most solid foundations of modern physics; nonlocality would put it at risk. Is there any other way out of Bell’s theorem? This is where the peculiar and embarrassing bit comes in. For a long time, some physicists claimed that there was another assumption in Bell’s proof, that of hidden instruction sets. Don’t assume that there are any hidden instructions in the roulette balls at all, the argument went, and Bell’s theorem has no force. But this isn’t correct. We didn’t assume that there were any instructions in the roulette balls, at least not at the start of the proof. Instead, we merely assumed locality, and this inevitably led us to the conclusion that there must be instructions in the roulette balls, in order to account for the perfect match between your results and Fatima’s when you were both using the same roulette wheels. If pairs of roulette balls always land on the same color, then either they’re sharing instruction sets from the start, or they’re somehow communicating once they reach the roulette wheels. There’s no assumption of hidden instructions—there’s merely an assumption of locality, and the behavior of the roulette balls forced us to consider hidden instructions. So this isn't a good way to save locality. As John Bell, the physicist who discovered Bell’s theorem in 1964, said, “I don’t know any conception of locality which works with quantum mechanics. So I think we’re stuck with nonlocality.”

There might be other ways out of Bell's theorem: branching multiple universes, signals sent backward in time, or even vast cosmic conspiracies that go back to the Big Bang itself. But these options are even more strange and controversial than nonlocality. And some physicists have suggested denying the very idea of an external reality in order to avoid the conclusion that nature is nonlocal. But denying realism to break Bell’s proof invariably breaks the concept of locality as well—a Pyrrhic victory for those determined to keep physics local at all costs.

In short, Bell's theorem tells us that either there are subtle signals in nature that can travel faster than light, or something even weirder than that is going on. Either way, Bell's theorem gives us a glimpse at the true face of the universe, revealing a world that is utterly different from our everyday perspective on reality.

---

This is just one glimpse of the bewildering subject at the edge of physics known as quantum foundations. There’s more—there’s a whole history of interpersonal clashes and political struggles among the physicists grappling with the very strangest concepts science has to offer, and a tantalizing challenge to the future of quantum physics.

If you’d like to read more about this, you should check out my book on the century-long search to understand what quantum physics is actually telling us about the world:

What is Real? The Unfinished Quest for the Meaning of Quantum Physics

---

Credits

Writing, design, illustrations, and code by
Adam Becker

Illustrations by
Nick James

Special thanks to
Glen Chiacchieri, Nicky Case, Peter Tallack, and TJ Kelleher.

This presentation of Bell's theorem is based primarily upon the excellent paper Is the Moon There When Nobody Looks? by N. David Mermin. However, the creators of this website are solely responsible for any errors herein.

The research and writing of What is Real? was made possible in part by a generous grant from the Alfred P. Sloan Foundation's Public Understanding of Science and Technology Program.

Copyright 2018 by Adam Becker. The written content of this website, along with the images (other than the photo of John Bell and the front cover of What is Real?) are all available under the CC BY 4.0 license. The underlying code is available under the MIT license, and may be found here.

If you liked this, please share it!